Time-dependent optimal control of the linear scalar wave equation¶

Section author: Steven Vandekerckhove <Steven.Vandekerckhove@kuleuven.be>

Problem definition¶

The problem is to minimise the following tracking-type functional

$J(y, u) = \frac{1}{2} \int_{0}^T | u(L, t) - u_\text{obs}(L, t) |^2 \, \, \mathrm{d}t,$

subjected to the time-dependent scalar wave equation equation

$u_{tt} - c^2 u_{xx} &= 0 \qquad \mathrm{in} \, \Omega \times (0, T), \\ u(x, 0) &= 0, \\ u(0, t) &= s(t), \\ u(L, t) &= 0,$

where $c$ is the wave speed and $\Omega = \left[0, L\right]$ is a one dimensional domain, for a given source function $s(t) = \sin(\omega t)$ :

In particular, we aim to

$\min J(u, \omega) \textrm{ over } (u, \omega).$

Discretization¶

Using a classic central difference for discretizing in time, with time step $\Delta t$ , the time-discretized differential equation reads: for a given $s^n$ , for each time step $n$ , find $u^{n+1}$ such that

$\frac{u^{n+1} - 2 u^n + u^{n-1}}{\Delta t^2} - c^2 u^n_{xx} &= 0, \\ u(0, t^n) = s(t^n) &= s^n.$

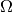Let $U$ be the space of continuous piecewise linear functions. Multiplying by test functions $v \in U$ , integrating by parts over $\Omega$ , the problem reads: find $u_h^{n} \in U$ such that

$\langle \frac{u^{n+1} - 2 u^n + u^{n-1}}{\Delta t^2}, v \rangle + \langle c^2 u^n_x, v_x \rangle &= 0,$

hold for all $v \in U$ .

Implementation¶

We start our implementation by importing the dolfin and dolfin_adjoint modules, together with the numpy and sys modules, for handeling storage and ui:

from dolfin import *
from dolfin_adjoint import *
import numpy as np
import os, sys

Next, we prepare the mesh,

mesh = UnitIntervalMesh(50)

and set a time step size:

k = Constant(1e-3)

Since we want to add boundary conditions only on the left hand side, and make observations on the left hand side, we have to identify both sides separately:

# Compile sub domains for boundaries
left  = CompiledSubDomain("near(x[0], 0.)")
right = CompiledSubDomain("near(x[0], 1.)")

# Label boundaries, required for the objective
boundary_parts = MeshFunction("size_t", mesh, mesh.topology().dim()-1)
left.mark(boundary_parts, 0)
right.mark(boundary_parts, 1)
ds = Measure("ds")[boundary_parts]

Then, an expression is built for the time dependent source term. We need to provide member functions for evaluating the function and its derivative.

class Source(Expression):
    def __init__(self, t, omega=Constant(2e2)):
        """ Construct the source function """
        self.t = t
        self.omega = omega

    def eval(self, value, x):
        """ Evaluate the expression """
        if x[0] < 1e-15:
            value[0] = np.sin(float(self.omega)*self.t)
        else:
            value[0] = 0.

    def deval(self, value, x, coeff):
        """ Evaluate the derivative of the expression """
        assert coeff == self.omega, "Given coeff must be the start time"
        if x[0] < 1e-15:
            value[0] = self.t*np.cos(float(self.omega)*self.t)
        else:
            value[0] = 0.

    def dependencies(self):
        """ List the dependencies of which derivatives are taken """
        return [self.omega]

    def copy(self):
        """ Return a copy of itself """
        return Source(self.t, self.omega)

Before the inverse problem can be solved, we have to implement the forward problem:

def forward(excitation, c=Constant(1.), record=False, annotate=False):
    # Define function space
    U = FunctionSpace(mesh, "Lagrange", 1)

    # Set up initial values
    u0 = interpolate(Expression("0."), U, name = "u0", annotate = annotate)
    u1 = interpolate(Expression("0."), U, name = "u1", annotate = annotate)

    # Define test and trial functions
    v = TestFunction(U)
    u = TrialFunction(U)

    # Define variational formulation
    udot = (u - 2.*u1 + u0)
    uold = (0.25*u + 0.5*u1 +0.25*u0)
    F = (udot*v+k*k*c*c*uold.dx(0)*v.dx(0))*dx - u*v*ds(0) + excitation*v*ds(0)
    a = lhs(F)
    L = rhs(F)

    # Prepare solution
    u = Function(U, name = "u", annotate = annotate)

    # The actual timestepping
    if record: rec = [u1(1.),]
    i = 1
    t = 0.0        # Initial time
    T = 3.e-1      # Final time
    times = [t,]
    if annotate: adj_start_timestep()
    while t < T - .5*float(k):
        print t
        excitation.t = t + float(k)
        solve(a == L, u, annotate = annotate)
        u0.assign(u1, annotate = annotate)
        u1.assign(u, annotate = annotate)

        t = i*float(k)
        times.append(t)
        if record:
            rec.append(u1(1.0))
            plot(u)
        if annotate: adj_inc_timestep(t, t > T - .5*float(k))
        i += 1

    if record:
        np.savetxt("recorded.txt", rec)

    return u1, times

Note that the forward solver has been implemented as straight forward as possible, with litte attention for efficiency. E.g., a significant speed-up could be realized by re-using the factorization of linear system.

Also a function is defined to assemble the objective

def objective(times, u, observations):
    combined = zip(times, observations)
    area = times[-1] - times[0]
    M = len(times)
    I = area/M*sum(inner(u - u_obs, u - u_obs)*ds(1)*dt[t]
                   for (t, u_obs) in combined)
    return I

Now we can have a look at the optimization procedure

def optimize(dbg=False):
    # Define the control
    source = Source(t = 0.0, omega = Constant(190))

    # Execute first time to annotate and record the tape
    u, times = forward(source, 2*DOLFIN_PI, False, True)

    if dbg:
        # Check the recorded tape
        success = replay_dolfin(tol = 0.0, stop = True)
        print "replay: ", success

        # for the equations recorded on the forward run
        adj_html("forward.html", "forward")
        # for the equations to be assembled on the adjoint run
        adj_html("adjoint.html", "adjoint")

    # Load references
    refs = np.loadtxt("recorded.txt")

    # create noise to references
    gamma = 1.e-5
    if gamma > 0:
        noise = np.random.normal(0, gamma, refs.shape[0])

        # add noise to the refs
        refs += noise

    # map refs to be constant
    refs = map(Constant, refs)

    # Define the controls
    controls = [Control(c) for c in source.dependencies()]

    Jform = objective(times, u, refs)
    J = Functional(Jform)

    # compute the gradient
    dJd0 = compute_gradient(J, controls)
    print float(dJd0[0])

    # Prepare the reduced functional
    reduced_functional = ReducedFunctional(J, controls, eval_cb_post = eval_cb)

    # Run the optimisation
    omega_opt = minimize(reduced_functional, method = "L-BFGS-B",\
                     tol=1.0e-12, options = {"disp": True,"gtol":1.0e-12})

    # Print the obtained optimal value for the controls
    print "omega = %f" %float(omega_opt)

The code can be run as follows:

""" Compute  a reference solution (once) """
Source = source(t = 0.0, omega = Constant(2e2))
forward(Source, 2*DOLFIN_PI, True)

""" Start the optimization procedure """
optimize()

The complete code can be downloaded here.

Comments¶

Running the code results in an approximation for the optimal value for $\omega = 199.999986$ , which is correct up to the noise level.